
Let’s see, what is the power factor? And hence we will see the difference between KVA and KW.
First let’s see, what is the power factor?
In simple words, the Power factor is a measure of the effective use of electric power. That means the more the power factor, the better the power usage.
Power factor is nothing but the angle between voltage and current. Which is a phase difference between voltage and current. Hence power factor is directly related to the phase difference between voltage and current. Here we can see a phasor diagram of voltage and current of AC power supply. If we consider voltage as a reference, and Φ as the angle between voltage and current. Then power factor is cos of Φ.
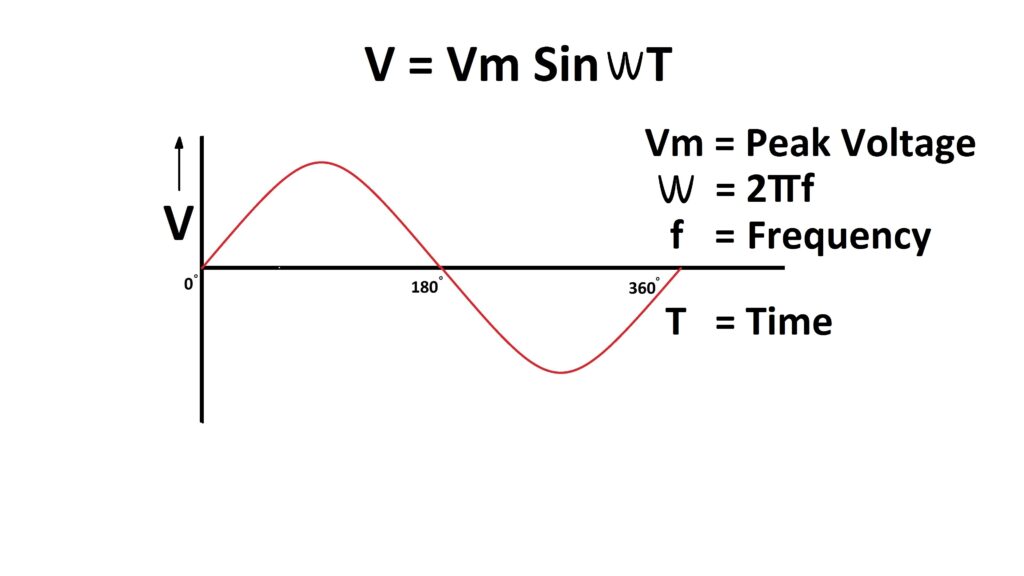
Now let’s consider waveforms of voltage and current. This is a voltage waveform.
The voltage equation is
V=VmsinωT
Where Vm=peak value of voltage
ω=2πf, where f is frequency & T is time
Current equations will be different based on the phase difference between voltage and current.
1. Current in phase with the voltage (Φ=0):
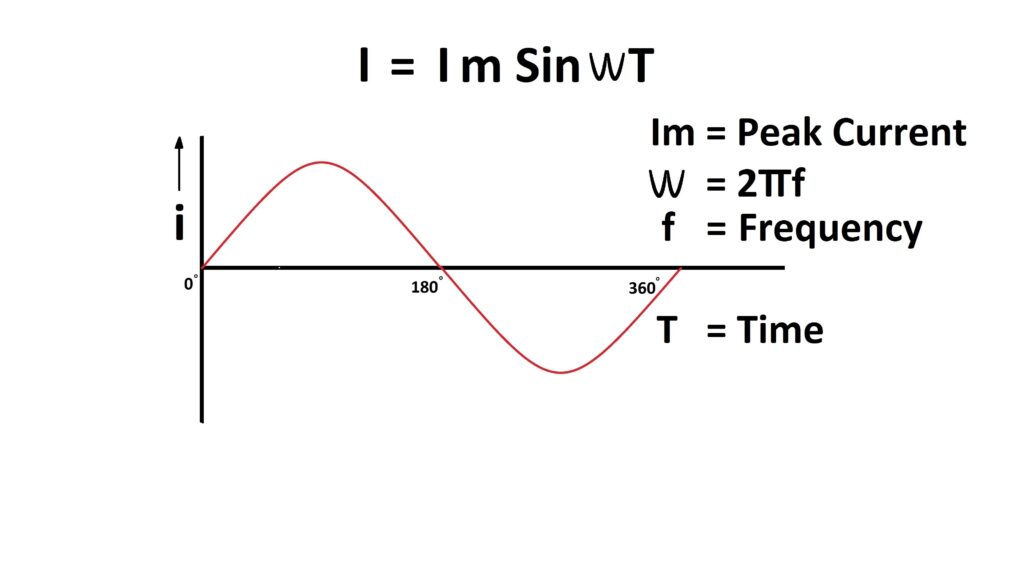
This means the phase difference between voltage and current is zero. This Means Φ is zero.
Hence current equation is
I=ImsinωT
Similar equation and phasor diagram as that of voltage.
Where
Im= Peak value of current. ω=2πf. f is frequency. T is time.
Current in phase with the voltage.
2. Current leads the voltage (Φ+Ve):

This means that Φ is positive.
Hence equation of current is
I=Imsin(ωT+Φ)
Current leads voltage in capacitive circuit or load.
Current leads the voltage.
3. Current lags voltage (Φ-Ve):

This means that Φ is negative.
Hence equation of current is
I=Imsin(ωT-Φ)
Current lags voltage in inductive circuit or load. Generally, any household or industrial load is inductive. Current lags voltage.
Now let’s see why there is a phase difference between voltage and current of AC power in the first place?
As we know that phase difference is nothing but the time difference between voltage and current propagation. The phase difference is mainly due to the frequency of the AC power supply. Due to its alternating nature AC power has frequency which causes phase difference between voltage and current, in both inductive and capacitive circuits. In a DC power circuit there is no frequency, hence no phase difference between voltage and current, and hence power factor is unity.
What is Active Power? And what is Reactive Power?
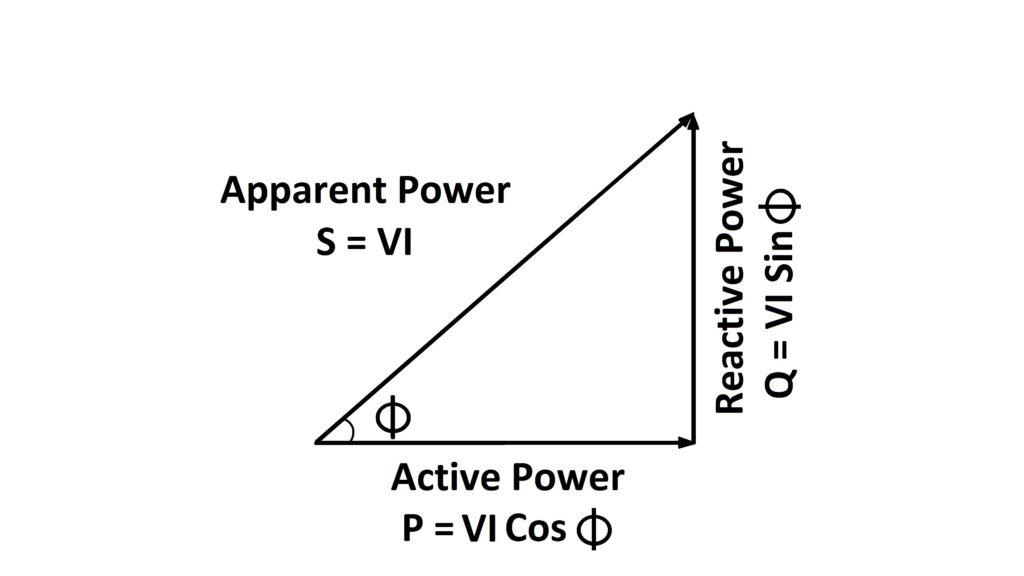
In simple words, active power is useful to power by which load performs its function. Reactive power exists mainly due to inductive and capacitive properties of circuit or load which is consumed for charging circuits or loads. This power moves back and forth between source and load. Hence reactive power does not contribute directly to load function.
For better understanding let’s see the power triangle. In this power triangle, this is active power denoted as P, this is reactive power denoted as Q, and this is the vector addition of active and reactive power called apparent power denoted as S. As we saw only this active power is useful to power. Again these three types of power exist because of phase angle which is the phase difference between voltage and current. Hence active and reactive powers are also related directly to the power factor.
Now let’s look at the relationship between reactive power.
As we know active power
P = VIcosΦ
And reactive power
Q = VIsinΦ
Where
V is voltage, I is current and Phi is a phase difference between voltage and current.
Also in the diagram, we can see that apparent power is the vector addition of active and reactive power.
Hence apparent power
S = Vector P + Vector Q
So
S = VIcosΦ + VIsinΦ
Also, it is represented as
S = P + J Q
And in magnitude or scalar form it is given as
S = √(P²+Q²)
These equations are used in many active and reactive power-related calculations.